In a prior post I asked the following question:
find x,y,z positive natural numbers such that the following is true:
$$ \frac{x}{y+z} + \frac{y}{x+z} + \frac{z}{x+y} = 4. $$
I first saw the question in a more fun way:
I did not put the answer in the post (should I have? That was the meta question.)
The question has an infinite number of (x,y,z) that work, so I'll just give the least one:
x= 154476802108746166441951315019919837485664325669565431700026634898253202035277999
y = 36875131794129999827197811565225474825492979968971970996283137471637224634055579
z = 4373612677928697257861252602371390152816537558161613618621437993378423467772036
1) For details on how you could have found the answer see here. Or watch a YouTube video on it here.
2) Did I really expect my readers to get this one? Note that I posted it on April Fools Day, though it is a legit problem with a legit answer.
3) The image that says that 95% of all people couldn't solve it---I wonder what their sample size was and where it was drawn from. I suspect that among mathematicians 99% or more can't solve it.
4) Comments on the comments I got:
a) Austin Buchanan says that Wolfram Alpha says NO SOLUTION. I wonder if Wolfram Alpha cannot handle numbers of this size.
b) Anonymous right after Austin had a comment that I MISREAD as saying that they found it using a python program. I asked that person to email me, and it turns out that NO-- they recalled where to look (on the web I assume).
c) Several commenters solved it by looking at the web. Math Overflow and Quora had solutions. So did other places. This may make the meta question should a blogger post the solution a moot point for a well known problem. If you get a problem off the web its quite likely its well known, or at least well enough known, to have the answer also on the web. If you make up a problem yourself then its harder to tell.
5) I think its a very hard problem to solve unless you have the prior KNOWLEDGE to solve it, so it would not be a good math competition problem.
6) The cute pictures of fruit in the presentation of the problem makes it LOOK like its a cute problem. It not.
7) Only one comment on the meta question about should a blogger post the solution at the same time as the problem (There were more comments about the unimportant question of whether 0 is a natural number.) The one comment says that a blogger SHOULD NOT - let the reader enjoy/agonize for a while. I agree.
8) Determining if a given math problem is interesting is a hard problem; however, that will be a topic for another blog. (Tip for young bloggers, if there are any (blogs are so 2010): If you do ONE idea per blog then your blog can last longer.)
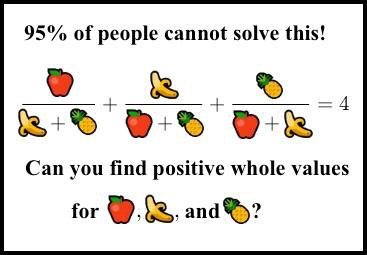
You should post a hint about the hardness of the problem I think. This would probably be a double starred question, though not a research problem, in a Knuth book.
ReplyDeleteNormally yes, but this was an April Fools Day post-- give a cute sounding problem with a cute picture (which i did not draw-it was at the website I found it) for a really hard problem.
DeleteMathematica more correctly than Wolfram Alpha does give a “semisymbolic” solution which would, purportedly, allow you to compute the solution. It certainly does not tell you that there are no solutions, which most likely it would if there really were no solutions. I myself would not know how to take this solution and produce numbers from it.
ReplyDeleteAnother meta question here is, given that eliptic curves work to solve this problem, is that because eliptic curves work for a lot of simple problems, or did the bloke that came up with the problem work back from eliptic curve ideas to construct an innocent-looking problem?
ReplyDeleteexcellent question to which I do not know the answer. I often have a trick and build a problem around it. That makes it hard for me to know how hard it is.
DeleteI worked it out long enough to get to a place where I knew I *could* get to an answer but was *wise enough* to just wait for you to post the answer.
ReplyDeleteIf we replace 4 with n, for what values of n does there exist a solution? What is so special about 4?
ReplyDeleteConsidering the way the question in the image is phrased: "can you find ... ?" I was trying to work towards a yes/no answer. Proving existence/non-existence might be a lot easier than actually finding the numbers.
ReplyDeleteThat said, while I recognised it as an elliptic curve I know very little about that subject, so I was hoping there might be a neat trick I might stumble into.
I think that the original whimsical formatting sort of suggested that this wasn't that hard a problem. In that sense, if this had been a homework problem I'd been assigned, I would have been annoyed. (Although I guess maybe the whimsical formatting would've been less likely.) The phrase "find positive whole values..." probably should have suggested to me that it was pretty tricky.
ReplyDeleteI think the video redeems the meme, though, as it suggests that if you know enough about elliptic curves, the problem is not that hideous. (I didn't solve it, but also didn't spend much effort on it, because I wasn't getting anywhere.)
(Bill) Agree, that the whimsical format makes it seem like its easy. Thats part of the April Fool Day Joke. Having said that, the whimiscal version is what I found on the web- I dont know what they were thinking.
ReplyDeleteTo clarify, the fact that it was April Fools means that I'm not bothered that you didn't include a "spoiler alert" when you posted the original meme.
DeleteAnother possible, much older, problem which seems related to me is Fermat writing that he had a "truly marvelous proof" of his Last Theorem (as it was called). I guess he didn't exactly say that it was easy... But I think that those who worked on / proved FLT might be a bit justifiably snarky about how Fermat phrased that.