1) Question: find x,y,z natural numbers such that the following is true:
$$ \frac{x}{y+z} + \frac{y}{x+z} + \frac{z}{x+y} = 4. $$
I was first presented the problem a more fun way:
(NOTE- a commenter pointed out that ``Natural Numbers'' and `Positive Whole Values' are different since some people (and I AM one of them) include 0 as a natural. SO- to clarify, I want x and y and z to be naturals that are \(\ge 1\). )
2) Meta Question: When a blogger poses a question like that should they also post the answer? Have a pointer to the answer? Not have an answer? Pros and Cons:
a) If you do not list the answer at all (or post it in a few days) then people will not be tempted to look at the answer. They have to really work on it. (Maybe they can find the answer on the web).
b) There are people whose curiosity far exceeds their ego. So they want to work on in for (say) 5 minutes and then LOOK AT THE ANSWER! I am one of those people.
c) When you first look at a problem and work on it you are curious. If you have to wait a few days to get the answer then you may lose interest.
I invite you to work on both the question and the meta question. I will not be blocking people who post the answer in the comments, so if you want to work on it you might not want to look at the answers.
I will post the answer in a few days.
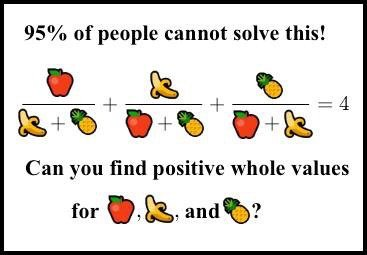
The two questions are not exactly the same if you are a logician or a computer scientist since their natural numbers include 0 which is excluded by the fruit version of the problem. (On the other hand, my elementary school textbook did not include 0 as a natural number and used the "whole" numbers as stated in the question for that case.)
ReplyDeleteZero is not a natural number. A set of Natural numbers contains counting numbers. We extend the set of Natural numbers by including zero. Such extension is called the set of Whole numbers.
ReplyDelete(Bill) Some textbooks define 0 as a natural. My only concern for this post is to clarify that I want x,y,z to be 1,2,3,... NOW- go work on the problem rather than comment about Natural vs Whole Numbers.
ReplyDeleteWolframalpha suggests that the problem has no solution https://www.wolframalpha.com/input?i=x+%2F+%28y%2Bz%29+%2B+y+%2F+%28x%2Bz%29+%2B+z+%2F+%28x%2By%29+%3D+4
ReplyDeleteThe last time a fun problem like this came up, I coded up some Python to run a few numbers, and, as someone who grew up coding assembler on machines that run at most 1 MIPS, I was completely freaked out at how fast interpreted Python runs on a 3.6 GHz i7. Times have changed.
ReplyDeleteThat time, I got the answer real quick. This one doesn't fall to brute force so easily. (Or maybe my programming is rustier than I think...)
But to answer the meta question: for problems like this, please don't give the answer (or a pointer to the answer), at least for a day or two. Let us agonize over it for a bit. At least here, an excuse to do some simple programming is appreciated, and maybe if I sleep on it, I'll think of something. Maybe.
By the way, I read a Comp. Sci. math textbook recently that used N for natural numbers including zero (since it was comp. sci.), but my impression was that it had to use N+ (natural numbers excluding zero) in the vast majority of cases. This made me think that maybe the math blokes know what they're doing...
Just for the record, the above comment was mine: I forgot to set the from field. I was wondering how much faster clearing fractions in the original expression, coding the resulting integer inequality it in 64-bit ints in C++, and searching for solutions would be, but the solution shows search wouldn't find it, no matter how sneaky I got about finding shared subexpressions and calculating them first...
Delete(Bill) Austin says there are no Solutions and Anoymous says that there are. Anonymous- please email me your solution (gasarch@umd.edu)
ReplyDelete9 11 -5
ReplyDelete(bill) The problem asked for positive naturals. However, I wonder if there is some way to, given an answer, find another answer with bigger values, so yours could be a starting point for finding a solution.
Delete11 4 -1
Deletea=4373612677928697257861252602371390152816537558161613618621437993378423467772036
ReplyDeleteb=36875131794129999827197811565225474825492979968971970996283137471637224634055579
c=154476802108746166441951315019919837485664325669565431700026634898253202035277999
https://mathoverflow.net/questions/227713/estimating-the-size-of-solutions-of-a-diophantine-equation
hint:
ReplyDeletethe smallest solution has 80 digits and requires advanced number theory (elliptic curves).
solution:
https://www.agftutoring.com/x-yz-y-xz-z-xy-4/
There's no need to exclude 0, since there's no integer solution with 0. E.g. setting z=0 results in x/y + y/x = 4, where x/y = 2 +- sqrt(3) which is not rational.
ReplyDeleteI had fun with this a couple of years ago. It took me a few weeks, working off and on. As noted above, I used some theory of Elliptic Curves. Here is a link to my solution: https://1drv.ms/b/s!AhtWOqognyHphyTQdcEXyyLNDEyq?e=mQ4fpu
ReplyDeleteAs for the meta question, I like it when people post an answer to puzzles they post. I have no problem if they post it a week later or something. I guess the posted answer shouldn't be "in your face" with the puzzle, so that one can choose to discipline one's self to work on it for a while.
PS This https://pari.math.u-bordeaux.fr/gpwasm.html can be used to check answers :-).
ReplyDeleteI haven't checked this solution, but Perplexity AI says the solution to the equation x/(y+z) + y/(x+z) + z/(x+y) = 4, where x, y, and z are positive integers, is as follows:
ReplyDeleteThe smallest positive integer solution to this equation is:
x = 36875131794129999827197811565225474825492979968971970996283137471637224634055579
y = 4373612677928697257861252602371390152816537558161613618621437993378423467772036
z = 154476802108746166441951315019919837485664325669565431700026634898253202035277999125
Stop using AI tools as if they're oracles, already.
DeleteFive seconds of Python (yes, Python has large integer arithmetics out of the box!) says that these numbers produce 3745.00642. At first, I thought "well, at least it's close to an integer" - then I realized it's off by three orders of magnitude.
"Python (yes, Python has large integer arithmetics out of the box!) says that these numbers produce 3745.00642."
DeletePython has large integers, but it also converts ratios to floating point. If you clear fractions and then do the calculation, you're more likely to be able to test solutions.
(i.e. set a = y+z, b = x+z and c = x+y, then
xbc + yac + zab = 4abc)
But, yes. The number immediately above are wrong. The numbers given earlier by another anonymous at 4:44 work fine in Python using the above cleared-fraction method.