Mr. Jaeger and The Scroll

There were three major influencers in my educational journey: Mike Sipser, my PhD advisor at Berkeley and MIT, Juris Hartmanis who founded the field of computational complexity and led me to it at Cornell, and Philip Jaeger, a math teacher at Millburn High School in New Jersey.

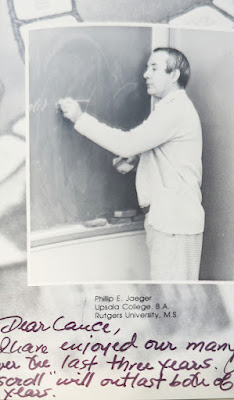Perhaps your "scroll" will outlast both of us.

I took two math courses with Philip Jaeger, Algebra II and Probability. Mr. Jaeger (I still can't call him Phil) also ran the computer room, a narrow room of three teletype machines where we saved programs on paper tape, where we would do simulations of poker hands for probability class among various other programming. He truly set me up for my future career. 

Mr. Jaeger was also the advisor of the computer club when I was president. 

That's me in the middle of the first photo, with Mr. Jaeger on my right.

Sometime during my high school years I took one of the rolls used in the teletype machine and wrote down a lengthy formula. According to Mr. Jaeger, the formula is for the area of a random triangle. I'm sure it made sense to me in high school.

The Scroll

The Scroll partially unscrolled

Another student Cheryl took the entire formula and put it entirely on an index card. Mr. Jaeger saved both the roll and the card.

The index card (actual size is 3x5 in)

Fast forward to 2023. Mr. Jaeger finds the roll and the card. His son, an academic in his own right, suggested that they track Cheryl and me down. I'm not hard to find. After some emails, they invited me to visit to pick up the roll. Last weekend I was in New Jersey visiting family so I did just that.

What great fun to talk to my old teacher, reminiscing about the high school people and times, and catching up after four decades. It was Mr. Jaeger who showed me the computer dating form that had me create a version for our high school.

I gave Mr. Jaeger a copy of my book and he gave me the scroll and the index card. (Cheryl, now a lawyer, wasn't interested in it). I safely brought it all home to Chicago along with all the memories. I dug up my old yearbook for first two photos above. The scroll will indeed outlast the both of us.

Mr. Jaeger, myself and the scroll.